অনুশীলনী 9.3
1. চিত্ৰত কোনো ত্ৰিভূজ ABC ৰ AD মধ্য়মাৰ ওপৰত E এটা যিকোনো বিন্দু। দেখুওৱা যে,
কালি (ABE) = কালি (ACE)


2. ABC ত্ৰিভূজৰ AD মধ্যনাৰ E মধ্য়বিন্দু। দেখুওৱা যে,
কালি (BED) = 1/4 কালি (ABC)


3. দেখুওৱা যে এটা সামান্তৰিকৰ কৰ্ণ দুটাই সামান্তৰিকটোক চাৰিটা সমান কালিৰ ত্ৰিভূজত ভাগ কৰে।


4. চিত্ৰত একে ভূমি AB ৰ ওপৰত ABC আৰু ABD দুটা ত্ৰিভূজ। যদি AB ৰেখাই Cd ৰেখাখণ্ডটোক O বিন্দুত সমিদ্বিখণ্ডিত কৰে, তেন্তে দেখুওৱা যে, কালি (ABC) = কালি (ABD)।


5. এটা ত্ৰিভূজ ABC ৰ BC, CA আৰু AB বাহুকেইটাৰ মধ্যবিন্দু যথাক্ৰমে D, E আৰু F। দেখুওৱা যে,
(i) BDEF এটা সামান্তৰিক
(ii) কালি (DEF) = 1/4 কালি (ABC)
(iii) কালি (BDEF) = 1/2 কালি (ABC)




6. চিত্ৰত ABCD চতুৰ্ভূজৰ কৰ্ণ AC আৰু BD য়ে O বিন্দুত ছেদ কৰিছে যাতে OB = OD।
যদি AB = CD, তেন্তে দেখুওৱা যে
(i) কালি (DOC) = কালি (AOB)
(ii) কালি (DCB) = কালি (ACB)
(iii) DA || CB অৰ্থাৎ ABCD এটা সামান্তৰিক।



7. ABC ত্ৰিভূজৰ AB আৰু AC বাহু দুটাৰ ওপৰত দুটা বিন্দু ক্ৰমে D আৰু E এনেদৰে লোৱা হৈছে যাতে কালি (DBC) = কালি (EBC)। প্ৰমাণ কৰা যে DE || BC।


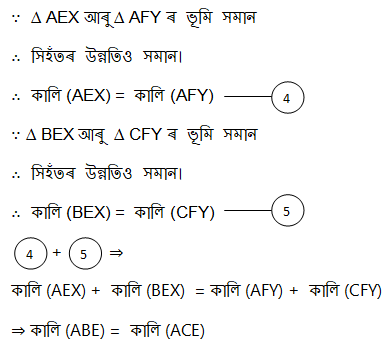
8. ABC ত্ৰিভূজৰ BC বাহুৰ সমান্তৰাল XY এডাল ৰেখা। যদি DE || BC আৰু CF || AB য়ে XY ক ক্ৰমে E আৰু F বিন্দুত কাটে, তেন্তে দেখুওৱা যে
কালি (ABE) = কালি (ACE)


9. ABCD এটা সামান্তৰিকৰ AB বাহুটোক যিকোনো এটা বিন্দু P লৈ বঢ়াই দিয়া হ’ল। এতিয়া A বিন্দুৰ মাজেৰে আৰু CP ৰ সমান্তৰালভাৱে টনা এটা ৰেখাই CB ৰ বৰ্ধিতাংশক Q বিন্দুত কাটিছে। এতিয়া PBQR সামান্তৰিকটো সম্পূৰ্ণ কৰা। দেখুওৱা যে
কালি (ABCD) = কালি (PBQR)
10. ABCD ট্ৰেপিজিয়ামৰ AB || DC। কৰ্ণ AC আৰু BD য়ে পৰস্পৰক O বিন্দুত কাটে। প্ৰমাণ কৰা যে, কালি (AOD) = কালি (BOC)।

11. চিত্ৰত ABCDE এটা পঞ্চভূজ। B বিন্দুৰ মাজেৰে AC ৰ সমান্তৰাল ৰেখা এটাই DC ৰ বৰ্দ্ধিতাংশৰ F বিন্দুত কাটিছে। দেখুওৱা যে
(i) কালি (ACB) = কালি (ACF)
(ii) কালি (AEDF) = কালি (ABCDE)

13. ABCD ট্ৰেপিজিয়ামৰ AB || DC। AC ৰ সমান্তৰাল এডাল ৰেখাই AB ক X আৰু BC ক Y বিন্দুত কাটিছে। প্ৰমাণ কৰা যে, কালি (ADX) = কালি (ACY)

14. চিত্ৰত AP || BQ || CR প্ৰমাণ কৰা যে,
কালি (AQC) = কালি (PBR)

15. ABCD চতুৰ্ভূজৰ AC আৰু BD কৰ্ণ দুডালে O বিন্দুত পৰস্পৰক এনেভাৱে কাটিছে যাতে কালি (AOD) = কালি (BOC)। প্ৰমাণ কৰা যে, ABCD এটা ট্ৰেপিজিয়াম।

16. চিত্ৰত কালি (DRC) = কালি (DPC), আৰু কালি (BDP) = কালি (ARC)। দেখুৱা যে ABCD আৰু DCPR চতুৰ্ভূজ দুয়োটাই ট্ৰেপিজিয়াম।

