ব্যৱহাৰিক জ্যামিতি
অনুশীলনী— 4.2
(1) এটা চতুৰ্ভুজ ABCD অংকন কৰা য’ত AB= 6 চেমি, BC= 7 চেমি, CD= 6.5 চেমি, DA= 5.5 চেমি আৰু < B= 105°
সমাধানঃ
AB= 6 চেমি
BC= 7 চেমি
CD= 6.5 চেমি
DA= 5.5 চেমি
<B= 105°

অংকন প্ৰণালী — A স্কেলৰ সহায়ত AB= 6 চেমি এডাল ৰেখাখণ্ড অঁকা হ’ল । <
B= 105° কোণ মান যন্ত দ্বাৰা অংকন কৰা হ’ল । B বিন্দুক কেন্দ্ৰ কৰি 7 চেমি ব্যাসাৰ্ধৰ বৃত্তচাপ অঁকা হ’ল আৰু C বিন্দু চ্নাক্ত কৰি BC অংশ কাটি লোৱা হ’ল । A বিন্দুক কেন্দ্ৰ কৰি DA= 5.5 চেমি ব্যাসাৰ্ধৰ বৃত্তচাপ অঁকা হ’ল । C বিন্দুক কেন্দ্ৰ কৰি 6.5 চেমি ব্যাসাৰ্ধৰ বৃত্তচাপ অংকা হ’ল যাতে আগৰ বৃত্তচাপক D বিন্দুত ছেদ কৰে । AD আৰু CD সংযোগ কৰা হ’ল আৰু চতুৰ্ভুজ ABCD পোৱা গ’ল।
(2) এটা চতুৰ্ভুজ ABCD অংকন কৰা য’ত AB= 5চেমি, BC= 4 চেমি, CD= 3.5 চেমি DA= 4.5 চেমি আৰু <C= 75°
সমাধান AB = 5 চেমি
BC= 4 চেমি
CD= 3.5 চেমি
DA= 4.5 চেমি
<C= 75°

অংকন প্ৰণালী
স্কেলৰ সহায়ত BC= 4 চেমি ৰেখাখণ্ড অংকন কৰা হ’ল । <C= 75° কোণমান যন্ত্ৰৰ দ্বাৰা অংকন কৰা হ’ল । C বিন্দুক কেন্দ্ৰ কৰি CD= 3.5 চেমি কাটি লোৱা হ’ল । B আৰু D বিন্দু দুটাক কেন্দ্ৰ কৰি 5 চেমি আৰু 4.5 চেমি ব্যাসাৰ্ধৰ দুটা বৃত্তচাপ অঁকা হ’ল । চাপ দুটা পৰস্পৰ A বিন্দুত ছেদ কৰিলে ।এতিয়া AB আৰু AD সংযোগ কৰা হ’ল । এতিয়া ABCD আকিঁবলগীয়া চতুৰ্ভুজ টো পোৱা গ’ল ।
(3) এটা চতুৰ্ভুজ ABCD অংকন কৰা য’ত AB= 4 চেমি, BC= 7 চেমি,< A= 105°, <B=75°, আৰু <C= 102°
সমাধান
AB= 4 চেমি, BC= 7 চেমি, <A= 105°, <B= 75° আৰু <C= 120°

অংকন প্ৰণালীঃ স্কেলৰ সহায় AB= 4 চেমি ৰেখাখণ্ড অংকন কৰা হ ল । A বিন্দুত 105° কোণ অংকন কৰা হল । B বিন্দুত 75° কোণ অংকন কৰা হ’ল । B বিন্দুক কেন্দ্ৰ কৰি 7 চেমি ব্যাসাৰ্ধৰ বৃত্তচাপ BX ৰশ্মিৰ ওপৰত অংকন কৰা হ’ল । BX আৰু বৃত্তচাপৰ ছেদ বিন্দুটোৱে C বিন্দুৰ অৱস্থান ( কাৰণ BC= 7 চেমি) এতিয়া BC সংযোগ কৰা হ’ল । C বিন্দুত 120° কোণ অংকন কৰা হ’ল আৰু CY ৰশ্মি অংকন কৰা হ’ল । AZ ৰশ্মি CY ৰশ্মিৰ ছেদ বিন্দুটোৱেই চতুৰ্ভুজৰ চতুৰ্থ শীৰ্ষ বিন্দু D ৰ অৱস্থান হৈছইল । AB আৰু CD সংযোগ কৰা হ’ল । এতিয়া আকিবলগীয়া ABCD চতুৰ্ভুজটো পোৱা গ’ল ।
(4) এটা চতুৰ্ভুজ EFGH অংকন কৰা য’ত EF= 5 চেমি, FG= 7.5 চেমি, LE= 90°, LG= 105° আৰু <H= 80°
সমাধান
EF= 5 চেমি, FG= 7.5 চেমি,<E= 90°,LG= 105° আৰু <H= 80°
অংকন প্ৰণালীঃ চতুৰ্ভুজ EFGH ত <E+ <F+ <G+<H= 360°
= 90°+<F+105°+80°=360°
= 275°+<F=360°
= <F=360°-275°=85°

স্কেলৰ সহায়ত EF=5 চেমি জোখত এডাল ৰেখা অংকন কৰা হ’ল । E বিন্দুত <FEY= 90° কোণটো অংকন কৰা হ’ল । F বিন্দুক <EFX=85° কোণটো অংকন কৰা হ’ল । F বিন্দুক <EFX=85°কোণ অংকন কৰা হ’ল । FX ৰ পৰা FG= 7 চেমি অংশ কাটি লোৱা হ’ল । G বিন্দুত <EGZ=105° কোণ অংকন কৰা হ’ল । GZ আৰু EY ৰশ্মিয়ে H বিন্দুত কটাকটি কৰিছে । কোণ মাপকৰ দ্বাৰা মাপি দেখা গ’ল যে ZH=80°আঁকা হ’ল । এতিয়া EFGH আঁকিবলগীয়া চতুৰ্ভুজ টো পোৱা গ’ল ।
(5) এটা সামান্তৰিক PQRS অংকন কৰা য’ত PQ=6 চেমি, QR=7 চেমি, আৰু <S=85°
সমাধান ঃ ইয়াত সামান্তৰিক PQRS ক=PQ=RS=6 চেমি,QR=7 চেমি আৰু <S=85°

অংকন প্ৰণালী
স্কেলৰ সহায়ত 6 চেমি দৈৰ্ঘ্যৰ এডাল ৰেখা খণ্ড অংকন কৰা হ’ল । S বিন্দুত <RSX=85° মাপৰ কোণটো অংকন কৰা হ’ল । SX ৰ পৰা SP=7 চেমি দৈৰ্ঘ্যৰ ৰেখাখণ্ড কাটি লোৱা হ’ল । এটা চাপ দুটা এইটোয়ে আনটোক ছেদ কৰিছে । তাৰ পাছত RQ আৰু PQ সংযোগ কৰা হ’ল । সংযোগ কৰা পাছত PQRS সামান্তৰিক পোৱা গ’ল ।
(6) এটা আয়ত LMNO অংকন কৰা য’ত LM=6 চেমি আৰু MN=4 চেমি ।
সমাধান — এটা আয়ত LMNO অংকন কৰিব লাগে য’ত LM= চেমি আৰু MN=4 চেমি
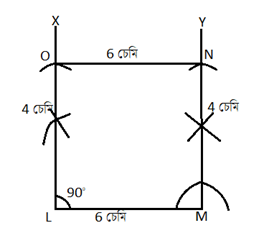
অংকন প্ৰণালী— স্কেলৰ সহায়ত LM=6 চেমি দৈৰ্ঘ্যৰ এডালৰেখাখণ্ড অংকন কৰা হ’ল । L বিন্দুত <MLX=90° আৰু M বিন্দুত <LMX=90° কোন দুটা অঁকা হ’ল । LX ৰ পৰা LO=4 চেমি আৰু MY ৰ পৰা MN=4 চেমি কাটি লোৱা হ’ল । তাৰ পাছত NO যোগ কৰা হ’ল । যোগ কৰা পাছত LMNO সেই আঁকিবলগীয়া আয়ত টো পোৱা গ’ল ।
(7) এটা চতুৰ্ভুজ PQRS অংকন কৰা য’ত PQ=6 চেমি, QR=7 চেমি, <Q=105° আৰু <R=80°
সমাধান ঃ
এটা PQRS চতুৰ্ভুজ অংকন কৰিব লাগে য’ত PQ=6 চেমি, QR=7 চেমি <Q=105° আৰু <R=80°

অংকন প্ৰণালী ঃ স্কেলৰ সহায় 7 চেমি=QR এডাল ৰেখা খণ্ড অংকন কৰা হ’ল । Q বিন্দুত কেন্দ্ৰ কৰি <RQX=105° কোন অংকন কৰা হ’ল আৰু R বিন্দুত কেন্দ্ৰ কৰি <QRY=80° কোন অংকন কৰা হ’ল । QX আৰু RY ৰ পৰা যথাক্ৰমে QP=6 চেমি আৰু RS=7.5 চেমি দৈৰ্ঘ্যৰ দুটাৰেখাখণ্ড কাটি লোৱা হ’ল । তাৰ পাছত PS সংযোগ কৰা হ’ল । PS সংযোগ কৰা পাছত PQRS আকিবলগীয়া চতুৰ্ভুজটো পোৱা গ’ল ।
(8) এটা চতুৰ্ভুজ ABCD অংকন কৰিব লাগে য’ত AB= 4.5 চেমি, BC=5.5 চেমি, CB=5 চেমি <B=68° আৰু <C=90°

অংকন প্ৰণালী ঃ
স্কেলৰ সহায়ত BC=5.5 চেমি দৈৰ্ঘ্যৰ এডাল ৰেখা খণ্ড অংকন কৰা হ’ল । B বিন্দুত কেন্দ্ৰ কৰি <CBX=68° কোন অংকন কৰা হ’ল আৰু <BCY=90° কোন অংকন কৰা হ’ল । BX আৰু CY ৰ পৰা AB=4.5 চেমি আৰু CP=5 চেমি দৈৰ্ঘ্যৰ ৰেখাখণ্ড কাটি লোৱা হ’ল । তাৰ পাছত AD সংযোগ কৰা হ’ল । সংযোগ কৰা পাছত ABCD আঁকিবলগীয়া চতুৰ্ভুজ টো পোৱা গ’ল ।
(9) এটা আয়ত অংকন কৰা যাৰ সন্নিহিত বাহুৰ দীঘ 5 চেমি আৰু 7 চেমি।
সমাধান ঃ
এটা আয়ত অংকন লাগে যাৰ সন্নিহিত বাহুৰ দীঘ 5 চেমি আৰু 7 চেমি ।

অংকন প্ৰণালী
AB=7 চেমি দৈৰ্ঘ্যৰ এডাল এডাল ৰেখা খণ্ড অংকন কৰা হ’ল । A বিন্দুত কেন্দ্ৰ কৰি ∠BAX কোন অংকন কৰা হ’ল আৰু B বিন্দুত কেন্দ্ৰ কৰি ∠ABY কোন অংকন কৰা হ’ল । AX ৰ পৰা AD=5 চেমি আৰু BY ৰ পৰা BC=5 চেমি কটা হ’ল । তাৰ পাছত CD সংযোগ কৰা হ’ল । সংযোগ কৰা পাছত ABCD আকিবলগীয়া আয়ত টো পোৱা গ’ল ।
