ব্যৱহাৰিক জ্যামিতি
অনুশীলনী 4.1
1. তলৰ চতুৰ্ভুজবোৰ অংকন কৰা।
(i) চতুৰ্ভুজ ABCD য’ত AB= 4চে.মি. ; BC= 6 চে.মি.; CD=5 চে.মি.; DA=5.5 চে.মি. আৰু কৰ্ণ= 7 চে.মি.
সমাধান :
চতুৰ্ভুজ ABCD
AB= 4
BC=6
CD=5

DA=5.5
কৰ্ম AC= 7 চেমি
অংকন প্ৰণালী—স্কেলৰ সহায়ত 7 চেমি জুখত এডাল ৰেখা অঁকা হ’ল । ৰেখা ডালৰ নাম AC ৰখা হ’ল । তাৰ পাছত A বিন্দুক কেন্দ্ৰ কৰি AB= 4 চেমি ব্যাসাৰ্ধলৈ এটা বৃত্ত চাপ অঁকা হ’ল । তাৰপাছত B বিন্দুক কেন্দ্ৰ কৰি BC= 6 চেমি ব্যাসাৰ্ধৰ লৈ আন এটা বৃত্তচাপ অঁকা হ’ল । বৃত্তচাপ দুটাই B বিন্দুক কটাকটি কৰিছে । AB আৰু BC যোগ কৰা হ’ল ।
আকৌ,
A আৰু C বিন্দুক কেন্দ্ৰ কৰি ক্ৰমে AD= 5.5 চেমি আৰু CD=5 চেমি ব্যাসাৰ্ধ লৈ দুটা বৃত্তচাপ অঁকা হ’ল । ইহঁতে D বিন্দুত কটাকটি কৰিলে । এতিয়া AD আৰু CD সংযোগ কৰা হ’ল ।
∴ ABC আৰু ∆ ADC লগ লগোৱাত আকিবলগীয়া চতুৰ্ভুজ টো পোৱা গ’ল ।
চতুৰ্ভুজ ABCD য’ত AB= 4 চেমি, BC=3 চেমি, DA= 2.8 চেমি, কৰ্ণ PR= 5.5 চেমি আৰু কৰ্ণ BD= 4.5 চেমি
সমাধানঃ

(ii) চতুৰ্ভুজ ABCD য’ত AB= 4 চেমি, BC= 3চেমি, DA= 2.8 চেমি, কৰ্ণ AC= 5 চেমি আৰু কৰ্ণ BD= 4.5 চেমি
সমাধানঃ
AB= 6 চেমি
BC= 3 চেমি
DA= 2.8 চেমি
কৰ্ণ AC= 5 চেমি
কৰ্ণ BD= 4.5 চেমি
অংকন প্ৰণালী
AB=4 চেমি ৰেখাখণ্ড অঁকা হ’ল । তাৰপাছত BC= 3 চেমি এডাল ৰেখা অঁকা হ’ল । তাৰ পাছত DA= 2.8 চেমি এডাল ৰেখা অঁকা হ’ল । A বিন্দুক কেন্দ্ৰ কৰি 5 চেমি ব্যাসাৰ্ধৰ এটা বৃত্ত চাপ অঁকা হ’ল । B বিন্দুক কেন্দ্ৰ কৰি 3 চেমি ব্যাসাৰ্ধৰ এটা চাপ অঁকা হ’ল । এই চাপে আগৰ চাপক C বিন্দুক কাটিছে । AC আৰু BC সংযোগ কৰা হ’ল । আকৌ A বিন্দুক কেন্দ্ৰ কৰি 2.8 চেমি ব্যাসাৰ্ধলৈ এটা বৃত্ত চাপ অঁকা হ’ল । B বিন্দুক কেন্দ্ৰ কৰি 4.5 চেমি ব্যাসাৰ্ধলৈ এটা বৃত্ত চাপ অঁকা হ’ল । এই চাপো আগৰ চাপক D বিন্দুত কাটিছে । BD, CD সংযোগ কৰা হ’ল ।
∴∆ ABCD সেই আঁকিবলগীয়া চতুৰ্ভুজটো পোৱা গ’ল ।
(iii) চতুৰ্ভুজ PQRS য’ত PQ= 4.5 চেমি, PS= 5.5 চেমি, RS= 5 চেমি, কৰ্ণ PR= 5.5 চেমি, আৰু কৰ্ণ QS=T চেমি ।
সমাধানঃ
QR= 4.5 চেমি
PS= 5.5 চেমি
RS= 5 চেমি
কৰ্ণ PR= 5.5 চেমি
কৰ্ণ QS= 7 চেমি

অংকন প্ৰণালী PR=5.5 চেমি ৰেখাখণ্ড অঁকা হ’ল । P বিন্দুক কেন্দ্ৰ কৰি 5.5 চেমি ব্যাসাৰ্ধ আৰু R বিন্দুক কেন্দ্ৰ কৰি 5 চেমি ব্যাসাৰ্ধলৈ দুটা বৃত্তচাপ অঁকা হ’ল । চাপ দুটা পৰস্পৰ S বিন্দুত ছেদ কৰিছে । PS আৰু RS যোগ কৰা হ’ল । R বিন্দুক কেন্দ্ৰ কৰি 4.5 চেমি আৰু 5 বিন্দুক কেন্দ্ৰ কৰি 7 চেমি ব্যাসাৰ্ধলৈ দুটা বৃত্ত চাপ অঁকা হ’ল । এই চাপ দুটা পৰস্পৰ Q বিন্দুত ছেদ কৰে । এতিয়া SQ, RQ আৰু PQ সংযোগ কৰা হ’ল । PQRS চতুৰ্ভুজটো হ’ল আকিবলগীয়া চতুৰ্ভুজ ।
(iv) সামান্তৰিক EFGH য’ত FG= 7 চেমি, GH=5.5 চেমি আৰু HF=8.5; চেমি
সমাধানঃ
FG= 7 চেমি
GH=5.5 চেমি
HF= 8.5 চেমি

অংকন প্ৰণালী
Ex ৰেখাখণ্ডৰ পৰা EF= 5.5 চেমি এটা বৃত্তচাপ কাটি লোৱা হ’ল । E ক কেন্দ্ৰ কৰি 7 চেমি এটা বৃত্তচাপ অঁকা হ’ল । আৰু F ক কেন্দ্ৰ কৰি 8.5 চেমি ব্যাসাৰ্ধৰ বৃত্তচাপ অঁকা হ’ল । এই চাত্ৰা দুটা H বিন্দুত ছেদ কৰিলে । EH আৰু HF সংযোগ কৰা হ’ল । F বিন্দুক কেন্দ্ৰ কৰি 7 চেমি ব্যাসাৰ্ধ আৰু H বিন্দুক কেন্দ্ৰ কৰি 5.5 চেমি ব্যাসাৰ্ধলৈ দুটা বৃত্তচাপ অংকন কৰা হ’ল । এই চাপ দুটা পৰস্পৰ G বিন্দুত ছেদ কৰিলে । HG আৰু GF সংযোগ কৰা হ’ল । ফলস্বৰূপে EFGH সামান্তৰিক পোৱা গ’ল ।
(V) ৰন্বাছ DEEG য’ত DE= 5 চেমি আৰু EG= 6.5 চেমি
সমাধান
DE= 5 চেমি
EG= 6.5 চেমি
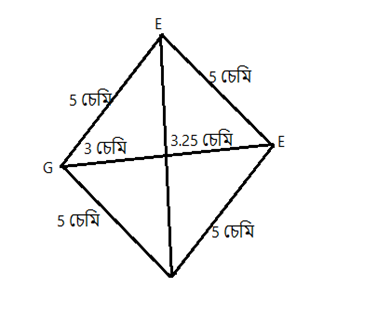
অংকন প্ৰণালী
স্কেলৰ সহায়ত 6.5 চেমি EG ৰেখাখণ্ড অঁকা হ’ল । G আৰু E ক কেন্দ্ৰ কৰি 5 চেমি ব্যাসা্ধৰ EG ৰ দুয়ো বিপৰীত দিশত চাৰিটা বৃত্তচাপ অঁকা হ ‘ল । ওপৰৰ চাপ দুটাৰ ছেদ বিন্দু ধৰা হ’ল F আৰু তলৰ চাপ দুটাৰ ছেদ বিন্দু ধৰা হ’ল D । এতিয়া DE, EF, FG আৰু GD সংযোগ কৰি DEFG ৰম্বাছ পোৱা গ’ল ।
(vi) ৰম্বাছ LMNO য’ত LN= 6 চেমি আৰু MO= 7 চেমি
সমাধানঃ
LN= 6 চেমি
MO= 7 চেমি

অংকন প্ৰণালী
স্কেলৰ সহায়ত 6 চেমি দৈৰ্ঘ্যৰ এটি ৰেখাখণ্ড LN অঁকা হ’ল । LN বাহুৰ মধ্যবিন্দুৰ নাম Q ৰখা হ’ল । কাটা কম্পাছৰ সহায়ত Q বিন্দুত কেন্দ্ৰ কৰি লম্ব সমদ্বিখণ্ডত অঁকা হ’ল আৰু ওপৰ দিশত 3.5 চেমি ব্যাসাৰ্ধৰ (MO আধা) দৈৰ্ঘ্যৰ দুয়োটা বৃত্তচাপে লম্ব দ্বিখণ্ডক ছেদ কৰা বিন্দু দুটাই হ’ব O আৰু M বিন্দুৰ অৱস্থান ILO, ON, NM, আৰু ML সংযোগ কৰি LMNO ৰম্বাছ পোৱা গ’ল ।